Next: Adjoint and types of Up: Operator Theory Previous: Infinite dimensional vector space Contents
Define convolution of two real valued Lebesgue measurable functions
![]() as
as
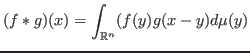
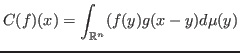
The same convolution operator can be recognized as an integral operator as well with kernel
![]() . With the same kernel, for
. With the same kernel, for ![]() this appears like a Hilbert-Schmidt operator. Let us first consider Schur's condition
this appears like a Hilbert-Schmidt operator. Let us first consider Schur's condition
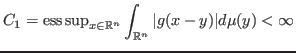
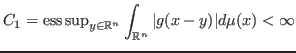
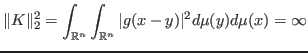
suku 2013-09-27