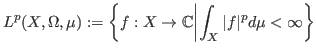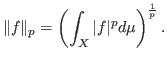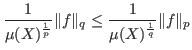Definition 3 (Measure space)
Let
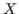
be a set and
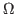
is a
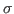
-algebra on
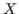
and
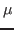
is a measure. Then for
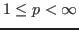
,
is a Banach space with respect to the norm, denoted by
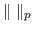
, called as ``
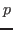
-norm", and defined as
For
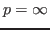
case,
is also a Banach space with respect to the norm, denoted by
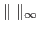
, called as ``essential supremum", and defined as
Note that those measurable functions, for which we can define the norm, are precisely collected in the appropriate space.